Prepare for exams with the Class 10 Mathematics Basic (Code 241) Previous Year Question Paper 2025 with Solution. The solved paper has been designed according to the new CBSE pattern and features step-by-step solutions to enable students to grasp the right method of answering each question. All major topics like Number Systems, Algebra, Geometry, Mensuration, and Statistics are covered in this paper to make it ideal for students who want to revise effectively and gain confidence. Download the PDF for practicing actual board-level questions and gauging your preparation level for the final exam. A resource one cannot do without for scoring well in the Maths Basic paper.
Series GE1FH
Question Paper Code 430/1/1 Set 1
MATHEMATICS (BASIC) – Solution Updating…
(Session 2024-25)
Time allowed : 3 hours
Maximum Marks : 80
General Instructions: Read the following instructions very carefully and strictly follow them:
(i) This question paper contains 38 questions. All questions are compulsory.
(ii) This question paper is divided into five Sections A, B, C, D and E.
(iii) In Section A, Questions no. 1 to 18 are multiple choice questions (MCQs) and questions number 19 and 20 are Assertion-Reason based questions of 1 mark each.
(iv) In Section B, Questions no. 21 to 25 are very short answer (VSA) type questions, carrying 2 marks each.
(v) In Section C, Questions no. 26 to 31 are short answer (SA) type questions, carrying 3 marks each.
(vi) In Section D, Questions no. 32 to 35 are long answer (LA) type questions carrying 5 marks each.
(vii) In Section E, Questions no. 36 to 38 are case study based questions carrying 4 marks each. Internal choice is provided in 2 marks questions in each case study.
(viii) There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, 2 questions in Section D and 3 questions in Section E.
(ix) Draw neat diagrams wherever required. Take = wherever required, if not stated.
(x) Use of calculator is not allowed.
SECTION A
This section has 20 Multiple Choice Questions (MCQs) carrying 1 mark each. 20X1=20
1. If the HCF of two positive integers a and b is 1, then their LCM is:
a) a + b
b) a
c) b
d) ab
2. The number √3 + is:
a) a rational number
b) an irrational number
c) an integer
d) a natural number
3. The discriminant of the quadratic equation x2 – 3x – 2 = 0 is:
a) 1
b) 17
c) √17
d) -√17
4. The equation x + 1/x = 3 (x ≠ 0) is expressed as a quadratic equation in the form of ax2 + bx + c = 0. The value of a – b + c is:
a) 5
b) 2
c) 1
d) -1
5. For a point (3, -5), the value of (abscissa -ordinate) is:
a) – 8
b) – 2
c) 2
d) 8
6. The mid-point of a line segment divides the line segment in the ratio:
a) 1 : 2
b) 2 : 1
c) 1 : 1
d) 1/2 : 2
7. Which of the following is not the criterion for similarity of triangles? (No correct Option – Bonus)
a) AAA
b) SSS
c) SAS
d) RHS
8. From the figures given below, which of the following is true about the measure of ∠P?
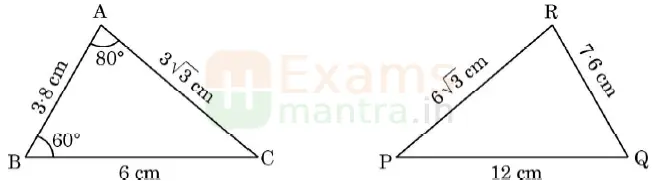
a) ∠P = 60°
b) ∠P = 80°
c) ∠P = 40°
d) The measure of ∠P cannot be determined
9. In the given figure, PA is a tangent to a circle with centre O. If OP = 10 cm, then the length of AP is:
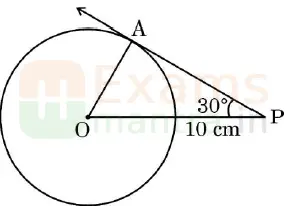
a) 10√3 cm
b) 20 cm
c) 5 cm
d) 5√3 cm
10. Which of the following statements is false?
a) tan 45° = cot 45°
b) sin 90° = tan 45°
c) sin 30° = cos 30°
d) sin 45° = cos 45°
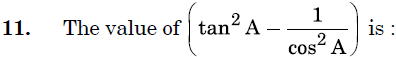
a) more than 1
b) 1
c) 0
d) – 1
12. In the given figure, which of the following angles represents the angle of depression?
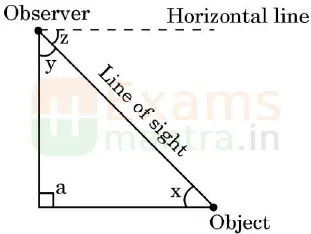
a) x
b) y
c) z
d) a
13. The perimeter of the shaded region in the given figure is:
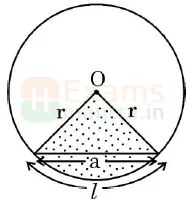
a) l
b) l + a
c) l + 2r
d) l + 2r + a
14. The ratio of the area of a quadrant of a circle to the area of the same circle is:
a) 1 : 2
b) 2 : 1
c) 1 : 4
d) 4 : 1
15. For which of the following solids is the lateral / curved surface area and total surface area the same ?
a) Cube
b) Cuboid
c) Hemisphere
d) Sphere
16. The class mark of the median class of the following data is:
| Class Interval | 10-25 | 25-40 | 40-55 | 55-70 | 70-85 | 85-100 |
| Frequency | 2 | 3 | 7 | 6 | 6 | 6 |
a) 40
b) 55
c) 47·5
d) 62·5
17. The following distribution shows the number of runs scored by some batsmen in test matches:
| Runs Scored | 3000-4000 | 4000-5000 | 5000-6000 | 6000-7000 |
| Number of Batsmen | 5 | 10 | 9 | 8 |
a) 3000
b) 4000
c) 5000
d) 6000
18. In a random experiment of throwing a die, which of the following is a sure event?
a) Getting a number between 1 and 6
b) Getting an odd number < 7
c) Getting an even number < 7
d) Getting a natural number < 7
Questions number 19 and 20 are Assertion and Reason based questions. Two statements are given, one labelled as Assertion (A) and the other is labelled as Reason (R). Select the correct answer to these questions from the codes (A), (B), (C) and (D) as given below.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false, but Reason (R) is true.
19. Assertion (A): For any two natural numbers a and b, the HCF of a and b is a factor of the LCM of a and b.
Reason (R): HCF of any two natural numbers divides both the numbers.
Ans: (a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
20. Assertion (A): The value of p for which the system of equations 4x + py + 8 = 0 and 2x + 2y + 2 = 0 is consistent is 4.
Reason (R): The system of equations a1x + b1y = c1 and a2x + b2y = c2 is consistent with infinitely many solutions, if a1/a2 = b1/b2 = c1/c2
Ans: (d) Assertion (A) is false, but Reason (R) is true.
SECTION B
This section has 5 Very Short Answer (VSA) type questions carrying 2 marks each. 5X2=10
22. (a) In the given figure, if PQ ∥ RS, then prove that △POQ ~ △SOR.
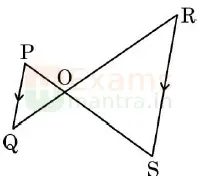
OR
22. In the given figure, △OSR ~ △OQP, ∠ROQ = 125° and ∠ORS = 70°. Find the measures of ∠OSR and ∠OQP.
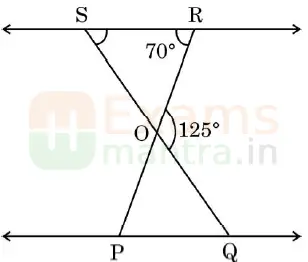
23. Two concentric circles are of radii 6 cm and 10 cm. Find the length of the chord of the larger circle which touches the smaller circle.
24. (a) Find the values of A and B (0 ≤ A ≤ 90° , 0 ≤ B ≤ 90° ), if tan (A + B) = 1 and tan (A-B) = 1/√3.
OR
(b) Prove that tan 45° = 1 geometrically.
25. A chord of a circle of diameter 20 cm subtends an angle of 60° at the centre of the circle. Find the area of the corresponding minor segment of the circle. (Use π = 3·14 and √3 = 1.73)
SECTION C
This section has 6 Short Answer (SA) type questions carrying 3 marks each. 6X3=18
26. (a) Prove that √3 is an irrational number.
OR
(b) The factor tree of a number x is shown below:
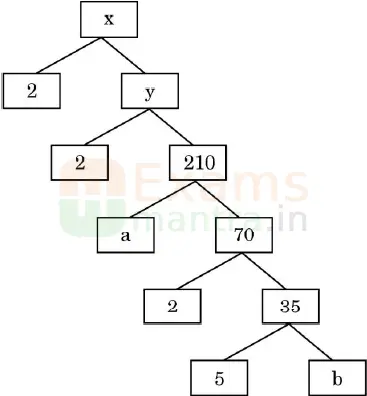
Find the values of x, y, a and b. Hence, write the product of the prime factors of the number x so obtained.
27. Find a quadratic polynomial whose sum and product of zeroes are 0 and 9, respectively. Also, find the zeroes of the polynomial so obtained.
28. (a) Solve the following system of equations graphically: x + 3y = 6; 2x – 3y = 12
OR
(b) x and y are complementary angles such that x : y = 1 : 2. Express the given information as a system of linear equations in two variables and hence solve it.
29. Prove that a rectangle circumscribing a circle is a square.
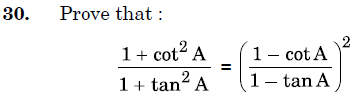
31. A lot consists of 200 pens of which 180 are good and the rest are defective. A customer will buy a pen if it is not defective. The shopkeeper draws a pen at random and gives it to the customer. What is the probability that the customer will not buy it ? Another lot of 100 pens containing 80 good pens is mixed with the previous lot of 200 pens. The shopkeeper now draws one pen at random from the entire lot and gives it to the customer. What is the probability that the customer will buy the pen?
SECTION D
This section has 4 Long Answer (LA) type questions carrying 5 marks each. 4X5=20
32. (a) The difference of the squares of two positive numbers is 180. The square of the smaller number is 8 times the greater number. Find the two numbers.
OR
(b) Find the value(s) of k for which the equation 2x2 + kx + 3 = 0 has real and equal roots. Hence, find the roots of the equations so obtained.
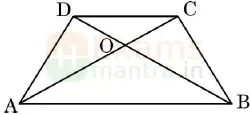
33. State “Basic Proportionality Theorem” and use it to prove: In a quadrilateral ABCD, diagonals AC and BD intersect each other at O such that AO/BO = CO/DO as shown in the given figure. Prove that ABCD is a trapezium.
34. (a) A toy is in the form of a cone surmounted on a hemisphere. The cone and hemisphere have the same radii. The height of the conical part of the toy is equal to the diameter of its base. If the radius of the conical part is 5 cm, find the volume of the toy.
OR
(b) A cubical block is surmounted by a hemisphere of radius 3·5 cm. What is the smallest possible length of the edge of the cube so that the hemisphere can totally lie on the cube ? Find the total surface area of the solid so formed.
35. The following data gives the information on the observed lifetime (in hours) of 200 electrical components:
| Lifetime (in hours) | Number of electrical components |
| 0-20 | 10 |
| 20-40 | 35 |
| 40-60 | 50 |
| 60-80 | 60 |
| 80-100 | 30 |
| 100-120 | 15 |
SECTION E
This section has 3 case study based questions carrying 4 marks each. 3X4=12
36. An injured bird was found on the roof of a building. The building is 15 m high. A fireman was called to rescue the bird. The fireman used an adjustable ladder to reach the roof. He placed the ladder in such a way that the ladder makes an angle of 60 with the ground in order to reach the roof.
Based on the above information, answer the following questions:
(i) Find the length of the ladder used by the fireman to reach the roof.
(ii) Find the distance of the point on the ground at which the ladder was fixed from the bottom of the building.
(iii) In order to avoid skidding, the fireman placed the ladder in such a way that the bottom of the ladder touches the base of the wall which is opposite to the building, making an angle of 30 with the ground.
(a) Draw a neat diagram to represent the above situation and hence find the width of the road between the building and the wall.
OR
(b) Find the length of the ladder used by the fireman in this case.
37. In a garden, saplings of rose flowers were planted at equal intervals to form a spiral pattern. The spiral is made up of successive semicircles, with centres alternatively at A and B, starting with centre at A, of radii 50 cm, 100 cm, 150 cm, ……. as shown in the figure given below. Spiral 1 has 10 flowers, Spiral 2 has 20 flowers, Spiral 3 has 30 flowers and so on.
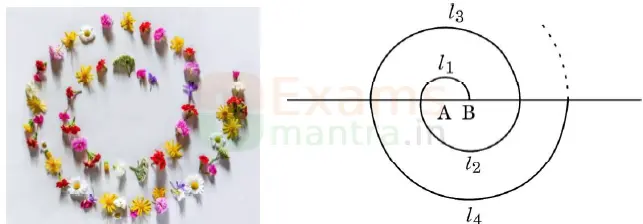
Based on the above information, answer the following questions:
(i) What is the radius of the 13th spiral?
(ii) If the radius of the nth spiral is 500 cm, find the value of n.
(iii) (a) Find the total number of saplings till the 11th spiral.
OR
(b) Till which spiral, will there be a total of 450 saplings?
38. In a society, there is a circular park having two gates. The gates are placed at points A(10, 20) and B(50, 50), as shown in the figure below. Two fountains are installed at points P and Q on AB such that AP = PQ = QB.
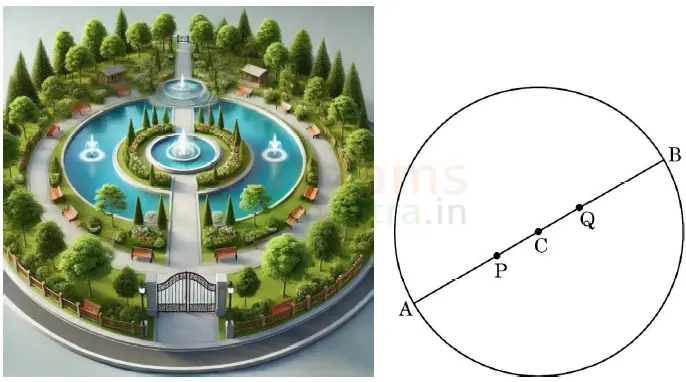
Based on the above information, answer the following questions:
(i) Find the coordinates of the centre C.
(ii) Find the radius of the circular park.
(iii) (a) Find the coordinates of the point P.
OR
(b) Find the distance of the fountain at Q from gate A.